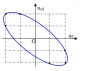
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm tu điện C và cuộn dây có trở thuần mắc nối tiếp. Hình bên dưới là đồ thị đường cong biểu diễn mối liên hệ của điện áp tức thời giữa hai đầu cuộn dây (Ucd) và điện áp tức thời giữa hai đầu tư điện C (uc) . Độ lệch pha giữa Ucd và Uc có giá trị là bao nhiêu ?
View attachment 195744
Bài này e nghĩ khoảng nửa tiếng mà cứ lòng vòng hoài ko ra kết quả? Giúp e với ạ?
Xét hai dao động điều hòa cùng tần số: $x_{1}=A_{1} \cos (\omega \cdot t+\varphi)$ và $x_{2}=A_{2} \cos (\omega \cdot t+\varphi+\Delta \varphi)$
Tìm hệ thức độc lập với thời gian liên hệ li độ của chúng.
Ta có: $x_{2}=A_{2} \cos (\omega \cdot t+\varphi) \cos \Delta \varphi-A_{2} \sin (\omega \cdot t+\varphi) \sin \Delta \varphi$
Hay: $x_{2}=\frac{A_{2}}{A_{1}} x_{1} \cos \Delta \varphi \pm A_{2} \sqrt{1-\frac{x_{1}^{2}}{A_{1}^{2}}} \sin \Delta \varphi \Leftrightarrow \pm \sqrt{1-\frac{x_{1}^{2}}{A_{1}^{2}}} \sin \Delta \varphi=\frac{x_{1}}{A_{1}} \cos \Delta \varphi-\frac{x_{2}}{A_{2}}$
Binh phương hai vế ta suy ra: $\frac{x_{1}^{2}}{A_{1}^{2}}+\frac{x_{2}^{2}}{A_{2}^{2}}-2 \frac{x_{1} x_{2}}{A_{1} A_{2}} \cos \Delta \varphi=\sin ^{2} \Delta \varphi$
Khi hai dao động vuông pha ta có: $\cos \Delta \varphi=0$ và $\sin ^{2} \Delta \varphi=1 \Rightarrow \frac{\mathrm{x}_{1}^{2}}{\mathrm{~A}_{1}^{2}}+\frac{\mathrm{x}_{2}^{2}}{\mathrm{~A}_{2}^{2}}=1$
Em có thể tham khảo cuộc tranh luận về vấn đề này
ở đây nhé, sẽ có sự thú vị đấy <:
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
