- 22 Tháng sáu 2017
- 2,357
- 4,161
- 589
- 20
- TP Hồ Chí Minh
- THPT Gia Định
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
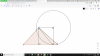
(Em vẽ hình xấu quá mong anh chị và các bạn thông cảm...)
Câu hỏi: Cho tam giác vuông cân ABC (AB=AC) có đường cao AH. Trên đoạn thẳng HC lấy điểm K rồi dựng hình chữ nhật AHKO. Lấy O làm tâm vẽ đường tròn bán kính OK, đường tròn này cắt cạnh AB tại D, cắt cạnh AC tại E. Gọi F là giao điểm thứ hai của (O) và đường thẳng AB. Chứng minh rằng:
a) Tam giác AEF là tam giác cân và DO vuông góc với OE.
b) Bốn điểm D,A,O,E cùng nằm trên một đường tròn.
tam giác ABC có: góc A =90 độ; AB=AC
=> góc B = góc C = 45 độ.
Lại có: AH là đường cao của tam giác ABC => AH cũng là đường trung trực vừa là tia phân giác của tam giác ABC
Và AH là đường trung tuyến ứng với cạnh huyền => BH=HC=AH=BC/2
Hình chữ nhật AHKO có AH=OK=R
=> góc B = góc C = 45 độ.
Lại có: AH là đường cao của tam giác ABC => AH cũng là đường trung trực vừa là tia phân giác của tam giác ABC
Và AH là đường trung tuyến ứng với cạnh huyền => BH=HC=AH=BC/2
Hình chữ nhật AHKO có AH=OK=R