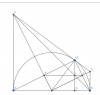
a) Ta có OE là đường trung bình nên OE // MB. Mà MB vuông góc với MA nên OE vuông góc với ME
Tương tự OF vuông góc với MF => OEMF là hình chữ nhật.
b) Tam giác cân AOM có OE là đường cao => OE là đường phân giác
=> MOE =AOE
Tam giác CAO = tam giác CMO (c.g.c)
=> CAO =CMO = 90 độ ( vì MC là tiếp tuyến tại M)
=> CA tiếp xúc với (O) tại A
Vì MAO = 30 độ nên AOC = 60 độ => [tex]AC=\sqrt{3}.AO=\sqrt{3}R=3\sqrt{3} (cm)[/tex]
c)CM như câu b) ta có DB = MD và AC=MC
Tam giác vuông COD có OM^2=MC.MD
R^2=AC.BD
Suy ra [tex]\frac{AC+BD}{2}\geq \sqrt{AC.BD}=R[/tex] (BĐT Cô-si)
[tex]S_{ACDB}=\frac{AC+BD}{2}.AB\geq 2R^2[/tex]
d) Ta có MF//OC => BI/BC=FI/FE
EF//AB => FI/FE=BG/BA
=> Tam giác BGI và tam giác BAC đồng dạng
=> GI vuông góc với AB=> MG vuông góc với EF
Lại có EI//AB, E là trung điểm AM nên I là trung điểm MG
=>...
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
