Vật lí 12 Bài 3: CON LẮC ĐƠN

[Triêu Dươngg]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài 3: CON LẮC ĐƠN
Phần 1: LÝ THUYẾT SGK VÀ CÁC CÂU HỎI LIÊN QUAN​

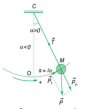
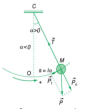
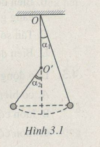
I. Con lắc đơn

+ Cấu tạo : Con lắc đơn là một cơ hệ gồm một vật nhỏ khối lượng [imath]m[/imath], treo ở đầu một sợi dây không dãn, khối lượng không đáng kể, có chiều dài [imath]l[/imath]. - Vị trí cân bằng của con lắc là vị trí mà dây treo có phương thẳng đứng. Con lắc sẽ đứng yên mãi ở vị trí này nếu lúc đầu nó đứng yên. - Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc rồi thả ra, ta thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng thẳng đứng đi qua điểm treo và vị trí ban đầu. + Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc rồi thả ra, ta thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng thẳng đứng đi qua điểm treo và vị trí ban đầu.

2. Phương trình dao động của con lắc đơn

Phương trình dao động li độ cong: [imath]S=S_0cos(\omega t+\varphi )[/imath]
Sử dụng hệ thức:[imath]S=l.\alpha[/imath] [liên hệ giữa độ dài cung và bán kính cung], chia 2 vế phương trình trên cho [imath]l[/imath], ta có phương trình dao động li độ góc: [imath]\alpha =\alpha _0cos(\omega t+\varphi )[/imath]

• Tần số ( rad/s): [imath]\omega =\sqrt{\dfrac{g}{l}}[/imath]
• Chu kì ( s) : [imath]T=\dfrac{2\pi }{\omega }=2\pi \sqrt{\dfrac{l}{g}}[/imath]
• Tần số (Hz) : [imath]f=\dfrac{1}{T}=\dfrac{1}{2\pi }.\sqrt{\dfrac{g}{l}}[/imath]

C1: Chứng tỏ rằng đối với những góc lệch nhỏ hơn [imath]20^0[/imath] thì độ chênh lệch giữa [imath]\sin \alpha[/imath] và [imath]\alpha (rad)[/imath] không đến [imath]1[/imath]%
Trả lời:
Ta kiểm nghiệm với các góc lệch nhỏ bằng [imath]20^0[/imath], ta có: [imath]\sin\alpha\approx \alpha[/imath] : [imath]\left\{\begin{matrix} \sin20^0=0,3420\\ 20^0=\dfrac{20\pi}{120}=0,2491(rad) \end{matrix}\right.[/imath]
Vậy độ chênh lệch giữa [imath]\sin \alpha[/imath] và [imath]\alpha (rad)[/imath] là: [imath]0,3491-0,3420=0,0071=0,7[/imath]%

C2: Có nhận xét gì về chu kì của con lắc đơn?
Trả lời:

• Chu kì ( s) : [imath]T=\dfrac{2\pi }{\omega }=2\pi \sqrt{\dfrac{l}{g}}[/imath]

Nhận xét:

• [imath]T[/imath] phụ thuộc vào chiều dài dây [imath]l[/imath] của dây và gia tốc trọng trường [imath]g[/imath] tại nơi đặt con lắc.
• [imath]T[/imath] tỉ lệ với căn bậc hai của chiều dài [imath]l[/imath] và tỉ lệ nghịch căn bậc hai của gia tốc trọng trường [imath]g[/imath].
• [imath]T[/imath] tăng khi chiều dài [imath]l[/imath] tăng hoặc gia tốc trọng trường giảm
• [imath]T[/imath] giảm khi chiều dài [imath]l[/imath] giảm hoặc gia tốc trọng trường tăng.

3. Năng lượng dao động của con lắc đơn

• Động năng: [imath]W_d=\dfrac{1}{2}mv^2[/imath]
• Thế năng trọng trường: [imath]W_t=mgl(1-cos\alpha )[/imath]
• Cơ năng: [imath]W=W_d+W_t[/imath]

Nhận xét : Nếu bỏ qua mọi ma sát và lực cản của môi trường thì cơ năng của con lắc đơn là một đại lượng bảo toàn [imath]W=const[/imath]

C3: Hãy mô tả một cách định tính sự biến đổi năng lượng của con lắc, khi nó đi từ vị trí biên về vị trí cân bằng và khi nó đi từ vị trí cân bằng ra vị trí biên.
Trả lời:
+ Tại vị trí cân bằng [imath]O (S = 0)[/imath]: thế năng [imath]W_t = 0[/imath]; động năng cực đại [imath]W_{d_{max}}[/imath].
+ Tại vị trí biên ([imath]x=\pm S[/imath]): thế năng cực đại [imath]W_{t_{max}}[/imath]; động năng [imath]W_d=0[/imath].
+ Khi vật đi từ vị trí biên về vị trí cân bằng thì thế năng giảm dần, động năng tăng dần.
+ Khi vật đi từ vị trí vị trí cân bằng ta biên thì thế năng tăng dần, động năng giảm dần.

4. Lực kéo về

• Lực kéo về (lực hồi phục) tác dụng lên vật nhỏ con lắc đơn có độ lớn: [imath]|F|=m\omega ^2s=mg\alpha[/imath]

5. Ứng dụng của con lắc đơn

+ Dùng để xác định gia tốc rơi tự do trong lĩnh vực địa chất

+ Các xác định gia tốc rơi tự do (gia tốc trọng trường)

• Đo thời gian [imath]t[/imath] của con lắc thực hiện được [imath]n[/imath] dao động toàn phần, sử dụng công thức [imath]T=\dfrac{t}{n}[/imath] để tính chu kì [imath]T[/imath].
• Sau đó tính gia tốc trọng trường bằng công thức [imath]g=\dfrac{4 \pi^2l}{T^2}[/imath]
• Lặp lại thí nghiệm nhiều lần, rồi tính giá trị trung bình [imath]g[/imath] ở các lần đo, ta được gia tốc rơi tự do tại nơi đó.

Xem thêm:
[Vật lí 7] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 8] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 9] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 10] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 11] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 12] HỆ THỐNG MỤC MỤC CÁC LỚP

 

[Triêu Dươngg]

Phần 2: CHỮA BÀI TẬP SGK​

Câu 1: Chứng minh rằng khi dao động nhỏ ([imath]\sin\alpha\approx \alpha(rad)[/imath]) , dao động của con lắc đơn là dao động điều hòa.

Lời giải:

Xét con lắc đơn như hình vẽ bên - Từ vị trí cân bằng kéo nhẹ quả cầu lệch khỏi vị trí cân bằng một góc nhỏ rồi thả ra. Con lắc dao động quanh vị trí cân bằng. - Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng từ trái sang phải. - Tai vị trí [imath]M[/imath] bất kì vật [imath]m[/imath] được xác định bởi li độ góc [imath]\alpha[/imath] hay về li độ cong là [imath]S=l.\alpha[/imath] - Tai vị trí [imath]M[/imath], vật chịu tác dụng trọng lực [imath]\overrightarrow{P}[/imath] và lực căng dây [imath]\overrightarrow{T}[/imath] Trong đó, [imath]\overrightarrow{P}[/imath] được phân tích thành phần như hình bên. Lực căng dây [imath]\overrightarrow{T}[/imath] và thành phần [imath]\overrightarrow{P_n}[/imath] vuông góc với đường đi nên không làm thay đổi tốc độ của vật. - Thành phần [imath]\overrightarrow{P_t}[/imath] là lực kéo về có giá trị: [imath]P_t=-mg\sin\alpha(1)[/imath] - Nếu li độ góc [imath]\alpha[/imath] nhỏ thì [imath]\sin\alpha\approx \alpha(rad)[/imath] ta có: [imath]P_t=-mg\alpha=-mg\dfrac{s}{l}[/imath] so sánh với lực kéo về của con lắc lò xo [imath]F=-kx[/imath] Ta thấy: [imath]\dfrac{mg}{l}[/imath] có vai trò của [imath]k\rightarrow \dfrac{l}{g}=\dfrac{m}{k}[/imath] Từ đây suy ra ĐPCM

Câu 2: Viết công thức tính chu kì của con lắc đơn khi dao động nhỏ.

Lời giải:

• Chu kì ( s) : [imath]T=\dfrac{2\pi }{\omega }=2\pi \sqrt{\dfrac{l}{g}}[/imath]

Câu 3: Viết biểu thức của động năng, thế năng và cơ năng của con lắc đơn ở vị trí có góc lệch [imath]\alpha[/imath] bất kì.

Lời giải:

• Động năng: [imath]W_d=\dfrac{1}{2}mv^2[/imath]
• Thế năng trọng trường: [imath]W_t=mgl(1-cos\alpha )[/imath]
• Cơ năng: [imath]W=W_d+W_t[/imath]

Câu 4: Chọn đáp án đúng.
Chu kì của con lắc đơn dao động nhỏ ([imath]\sin\alpha\approx \alpha(rad)[/imath]) là:
A. [imath]T=\dfrac{1}{2\pi}\sqrt{\dfrac{l}{g}}[/imath]
B. [imath]T=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{l}}[/imath]
C. [imath]T=\sqrt{2\pi \dfrac{l}{g}}[/imath]
D. [imath]T=2\pi \sqrt{\dfrac{l}{g}}[/imath]

Lời giải: Chọn [imath]D[/imath]

Câu 5: Hãy chọn đáp án đúng.
Một con lắc đơn dao động với biên độ góc nhỏ. Chu kì của con lắc không thay đổi khi:
A. thay đổi chiều dài của con lắc.
B. thay đổi gia tốc trọng trường.
C. tăng biên độ góc đến [imath]30^0[/imath].
D. thay đổi khối lượng của con lắc.

Lời giải: Chọn [imath]D[/imath]
Chu kì của con lắc đơn phụ thuộc vào [imath]l,g[/imath] và biên độ góc không phụ thuộc vào khối lượng [imath]m[/imath]. T không đổi khi thay đổi khối lượng [imath]m[/imath] của con lắc.

Câu 6: Một con lắc đơn được thả không vận tốc đầu từ li độ góc αo. Khi con lắc đi qua vị trí cân bằng thì tốc độ của quả cầu con lắc là bao nhiêu ?
A. [imath]v=\sqrt{gl(1-\cos\alpha_0)}[/imath]
B. [imath]v=\sqrt{2gl\cos\alpha_0}[/imath]
C. [imath]v=\sqrt{2gl(1-\cos\alpha_0)}[/imath]
D. [imath]v=\sqrt{gl\cos\alpha_0}[/imath]

Lời giải: Chọn [imath]C[/imath]

Câu 7: Một con lắc đơn dài [imath]l=2m[/imath], dao động điều hòa tại một nơi có gia tốc rơi tự do [imath]g = 9,8 m/s^2[/imath]. Hỏi con lắc thực hiện được bao nhiêu dao động toàn phần trong [imath]5[/imath] phút ?

Lời giải:
Chu kì: [imath]T=\dfrac{2\pi }{\omega }=2\pi \sqrt{\dfrac{l}{g}}=2,84s[/imath]
Số dao động toàn phần con lắc thực hiện được trong [imath]5[/imath] phút là: [imath]N=\dfrac{\Delta t}{T}\approx 106[/imath] ( Dao động)

Xem thêm:
[Vật lí 7] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 8] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 9] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 10] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 11] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 12] HỆ THỐNG MỤC MỤC CÁC LỚP

 

[Triêu Dươngg]

Phần 3: BÀI TẬP SÁCH BÀI TẬP
​

3.1: Kéo lệch con lắc đơn ra khỏi vị trí cân bằng một góc [imath]\alpha_0[/imath] rồi buông ra không vận tốc đầu. Chuyển động của con lắc đơn có thể coi như dao động điều hoà khi nào ?
A. Khi [imath]\alpha_0=60^0[/imath]
B. Khi [imath]\alpha_0=45^0[/imath]
C. Khi [imath]\alpha_0=30^0[/imath]
D. Khi [imath]\alpha_0[/imath] nhỏ sao cho: [imath]\sin\alpha_0\approx \alpha_0(rad)[/imath]

Lời giải: Chọn [imath]D[/imath]

3.4: Tại cùng một nơi trên mặt đất, nếu chu kì dao động điều hoà của con lắc đơn chiều dài [imath]l[/imath] là [imath]2s[/imath] thì chu kì dao động điều hoà của con lắc đơn chiều dài [imath]2l[/imath] là:
A. [imath]2\sqrt{2}s[/imath]
B. [imath]4s[/imath]
C. [imath]2s[/imath]
D. [imath]\sqrt{2}s[/imath]

Lời giải: Chọn [imath]A[/imath]
Chu kì sao động của con lắc đơn là: [imath]T=2\pi\sqrt{\dfrac{l}{g}}[/imath]
[imath]\Rightarrow T\sim \sqrt{l}\Rightarrow \dfrac{T_1}{T_2}=\sqrt{\dfrac{l_1}{l_2}}[/imath]
Từ đây thay dữ liệu tính ra đáp án

3.5: Một con lắc đơn dao động điều hoà với biên độ góc [imath]\alpha_0[/imath]. Tại li độ góc bằng bao nhiêu thì thế năng của con lắc bằng nửa động năng của con lắc ?
A. [imath]\dfrac{\alpha_0}{\sqrt{2}}[/imath]
B. [imath]\dfrac{\alpha_0}{2}[/imath]
C. [imath]\dfrac{\alpha_0}{\sqrt{3}}[/imath]
D. [imath]\dfrac{\alpha_0}{3}[/imath]

Lời giải: Chọn [imath]C[/imath]
Ta có: [imath]\left\{\begin{matrix} W_d=2W_t\\ W_d+W_t=W \end{matrix}\right.\Rightarrow W=3W_t[/imath]
Mà: [imath]\left\{\begin{matrix} W_t=mgl(1-\cos\alpha)\\ W=mgl(1-\cos\alpha_0) \end{matrix}\right.[/imath]
Khi [imath]\alpha[/imath] nhỏ: [imath]\left\{\begin{matrix} W_t\approx \dfrac{1}{2}mgl\alpha^2\\ W\approx \dfrac{1}{2}mgl\alpha_0^2 \end{matrix}\right.[/imath]
Từ đây [imath]\Rightarrow \alpha =\dfrac{\alpha_0}{\sqrt{3}}[/imath]

3.9: Một con lắc đơn được thả không vận tốc đầu từ vị trí biên có biên độ góc [imath]\alpha_0[/imath]. Khi con lắc đi qua vị trí có li độ góc [imath]\alpha[/imath] thì tốc độ của con lắc được tính bằng cồng thức nào? Bỏ qua mọi ma sát
A. [imath]v=\sqrt{2gl(\cos\alpha-\cos\alpha_0)}[/imath]
B. [imath]v=\sqrt{gl(\cos\alpha-\cos\alpha_0)}[/imath]
C. [imath]v=\sqrt{2gl(\cos\alpha_0-\cos\alpha)}[/imath]
D. [imath]v=\sqrt{2gl(1-\cos\alpha)}[/imath]

Lời giải: Chọn [imath]A[/imath]
Ta có: [imath]\left\{\begin{matrix} W_d=mgl(\cos\alpha-\cos\alpha_0)\\ W_d=\dfrac{1}{2}mv^2 \end{matrix}\right.\Rightarrow mgl(\cos\alpha-\cos\alpha_0)=\dfrac{1}{2}mv^2[/imath]
[imath]\Rightarrow v=\sqrt{2gl(\cos\alpha-\cos\alpha_0)}[/imath]

3.12: Một con lắc đơn gồm một quả cầu nhỏ có khối lượng [imath]50g[/imath] được treo vào đầu một sợi dây dài [imath]2m[/imath]. Lấy [imath]g=9,8m/s^2[/imath]
a) Tính chu kì dao động của con lắc khi biên độ góc nhỏ.
b) Kéo con lắc ra khỏi vị trí cân bằng đến vị trí có li độ góc [imath]\alpha=30^0[/imath] rồi buông ra không vận tốc đầu. Tính tốc độ của quả cầu và lực căng của dây khi con lắc qua vị trí cân bằng.

Lời giải:
a)
Chu kì sao động của con lắc đơn là: [imath]T=2\pi\sqrt{\dfrac{l}{g}}=2,8s[/imath]
b)
Ta có: [imath]\left\{\begin{matrix} W_d=mgl(\cos\alpha-\cos\alpha_0)\\ W_d=\dfrac{1}{2}mv^2 \end{matrix}\right.\Rightarrow mgl(\cos\alpha-\cos\alpha_0)=\dfrac{1}{2}mv^2[/imath]
[imath]\Rightarrow v=\sqrt{2gl(\cos\alpha-\cos\alpha_0)}=2,3(m/s)[/imath]
Áp dụng định luật II Newton: [imath]\overrightarrow{F}+ \overrightarrow{P}=m\overrightarrow{a}[/imath]
Chiếu theo phương hướng tâm: [imath]F-P=ma_{ht}=m\dfrac{v^2}{l}[/imath]
[imath]\Rightarrow F=P+m\dfrac{v^2}{l}[/imath]
[imath]\Leftrightarrow F=mg+2mg(1-\cos\alpha_0)[/imath]
[imath]\Leftrightarrow F=mg(3-2\cos\alpha_0)=0,62(N)[/imath]

3.15:

Một con lắc đơn dài [imath]2m[/imath]. Phía dưới điểm treo [imath]O[/imath], trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm [imath]O[/imath]′ cách [imath]O[/imath] một đoạn [imath]OO′=0,5m[/imath] , sao cho con lắc vấp vào đinh khi dao động (Hình.3.1). Kéo con lắc lệch khỏi phương thẳng đứng một góc [imath]\alpha_1=7^0[/imath] rồi thả không vận tốc đầu. Bỏ qua ma sát. Hãy tính: a) Biên độ của con lắc ở hai bên vị trí cân bằng. b) Chu kì dao động của con lắc. Lấy [imath]g=9,8m/s^2[/imath]

Lời giải:
a) Theo định luật bảo toàn cơ năng, ta suy ra hai vị trí biên [imath]A[/imath] và [imath]B[/imath] phải ở cùng một độ cao
Ta có: [imath]h_A=h_B\Rightarrow l(1-\cos \alpha_1)=\dfrac{3l}{4}(1-\cos\alpha_2 )[/imath]
[imath]\Rightarrow \cos\alpha_2=\dfrac{1}{3}(4\cos\alpha_1-1)=8,1^0[/imath]
b) Ta có: [imath]T=\dfrac{T_1+T_2}{2}=2\pi\sqrt{\dfrac{l}{g}}+2\pi\sqrt{\dfrac{3l}{g}}=2,65s[/imath]

Xem thêm:
[Vật lí 7] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 8] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 9] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 10] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 11] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 12] HỆ THỐNG MỤC MỤC CÁC LỚP