- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. Kiến thức cần nhớ:
* Hàm số bậc nhất là hàm có dạng: y=ax+b. Hàm số xác định với mọi x.
* Đồ thị: đồ thị của hàm số bậc nhất là 1 đường thẳng. Để vẽ được đồ thị thì cần 2 điểm mà đường thẳng đi qua. Thông thường, để nhanh nhất cho việc tính toán, ta chọn 2 điểm đấy là 2 điểm thuộc trục Ox, và Oy.
Gọi d là đường thẳng biểu diễn hàm số y=ax+b. (d) đi qua: A(0;b) thuộc Oy và B[tex](-\frac{b}{a};0)[/tex] thuộc Ox ( a khác 0)
Đặc biệt: với a=0, ta có (d): y=b là 1 đường thẳng song song với Ox.
a được gọi là hệ số góc của (d), a=[tex]tan\alpha[/tex], với [TEX]\alpha [/TEX] là góc tạo bởi (d) và trục Ox, lấy theo chiều dương Ox.
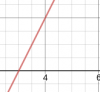
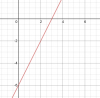
Trong hình trên là đồ thị hàm y=2x-6, góc [TEX]\alpha[/TEX] là 1 góc nhọn
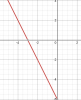
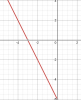
Còn ở hình này, đồ thị y=-2x-6, thì góc [TEX]\alpha[/TEX] là 1 góc tù.
+ Nhận xét: a>0 thì góc tạo bởi (d) và Ox là góc nhọn.
a<0 thì góc tạo bởi (d) và Ox là góc tù.
* Vị trí tương đối của 2 đường thẳng: cho 2 đường thẳng (d):y=[TEX]ax+b[/TEX] và (d'):[TEX]y=a'x+b'[/TEX]
Ta có:
+(d)//(d') nếu [TEX]a=a'[/TEX], [TEX]b \neq b'[/TEX]
+(d) vuông góc (d') nếu [TEX]a.a'=-1[/TEX]
+(d) trùng (d') nếu [TEX]a=a'[/TEX], [TEX]b = b'[/TEX]
+(d) cắt (d') nếu [TEX]a \neq a'[/TEX]
2. Bài tập:
1 số dạng bài tập thường gặp:
Xác định (d): y=ax+b biết:
a) (d) đi qua 2 điểm A(1;2) và B(4;5)
Giải: Do (d) qua A và B nên thay tọa độ của A và B vào y=ax+b phải thỏa mãn. Do đó ta có hệ:
[tex]\left\{\begin{matrix} 2=a+b\\ 5=4a+b \end{matrix}\right.[/tex] <=> a=1;b=1
Vậy pt của (d) là : [TEX]y=x+1[/TEX]
b) (d) đi qua A(1;3) và song song với (d1):[TEX]y=2x+3[/TEX]
Giải: Do (d)//(d1) nên a=2, do đó (d): y=2x+b.
Do A thuộc (d) nên: [TEX]3=2.1+b<=>b=1[/TEX]
=>pt của (d): [TEX]y=2x+1[/TEX]
c) (d) đi qua gốc tọa độ và tạo với trục Ox 1 góc 45 độ.
Giải: Ta có hệ số góc [tex]a=tan\alpha =tan45=1[/tex] => (d) có dạng: [TEX]y=x+b[/TEX]
Do (d) qua gốc tọa độ nên: [TEX]0=0+b<=>b=0[/TEX]
=> pt của (d) là: y=x
d) Tìm giao điểm của đường thẳng (d) tìm được ở câu b, với đường thẳng [TEX]y=3x+4[/TEX]
Giải: Khi tìm giao điểm, vì tọa độ của nó thỏa mãn đồng thời cả 2 phương trình, nên ta có phương trình hoành độ giao điểm: [TEX]2x+3=3x+4<=>x=-1[/TEX]
Thay x=-1 có [TEX]y=3.(-1)+4=1[/TEX]
Vậy tọa độ giao điểm cần tìm là A(-1;1)
Cơ bản là các dạng như vậy, chỉ cần nắm được lí thuyết là chúng ta có thể vận dụng để giải các bài tập của đề ra.
* Hàm số bậc nhất là hàm có dạng: y=ax+b. Hàm số xác định với mọi x.
* Đồ thị: đồ thị của hàm số bậc nhất là 1 đường thẳng. Để vẽ được đồ thị thì cần 2 điểm mà đường thẳng đi qua. Thông thường, để nhanh nhất cho việc tính toán, ta chọn 2 điểm đấy là 2 điểm thuộc trục Ox, và Oy.
Gọi d là đường thẳng biểu diễn hàm số y=ax+b. (d) đi qua: A(0;b) thuộc Oy và B[tex](-\frac{b}{a};0)[/tex] thuộc Ox ( a khác 0)
Đặc biệt: với a=0, ta có (d): y=b là 1 đường thẳng song song với Ox.
a được gọi là hệ số góc của (d), a=[tex]tan\alpha[/tex], với [TEX]\alpha [/TEX] là góc tạo bởi (d) và trục Ox, lấy theo chiều dương Ox.

Trong hình trên là đồ thị hàm y=2x-6, góc [TEX]\alpha[/TEX] là 1 góc nhọn

Còn ở hình này, đồ thị y=-2x-6, thì góc [TEX]\alpha[/TEX] là 1 góc tù.
+ Nhận xét: a>0 thì góc tạo bởi (d) và Ox là góc nhọn.
a<0 thì góc tạo bởi (d) và Ox là góc tù.
* Vị trí tương đối của 2 đường thẳng: cho 2 đường thẳng (d):y=[TEX]ax+b[/TEX] và (d'):[TEX]y=a'x+b'[/TEX]
Ta có:
+(d)//(d') nếu [TEX]a=a'[/TEX], [TEX]b \neq b'[/TEX]
+(d) vuông góc (d') nếu [TEX]a.a'=-1[/TEX]
+(d) trùng (d') nếu [TEX]a=a'[/TEX], [TEX]b = b'[/TEX]
+(d) cắt (d') nếu [TEX]a \neq a'[/TEX]
2. Bài tập:
1 số dạng bài tập thường gặp:
Xác định (d): y=ax+b biết:
a) (d) đi qua 2 điểm A(1;2) và B(4;5)
Giải: Do (d) qua A và B nên thay tọa độ của A và B vào y=ax+b phải thỏa mãn. Do đó ta có hệ:
[tex]\left\{\begin{matrix} 2=a+b\\ 5=4a+b \end{matrix}\right.[/tex] <=> a=1;b=1
Vậy pt của (d) là : [TEX]y=x+1[/TEX]
b) (d) đi qua A(1;3) và song song với (d1):[TEX]y=2x+3[/TEX]
Giải: Do (d)//(d1) nên a=2, do đó (d): y=2x+b.
Do A thuộc (d) nên: [TEX]3=2.1+b<=>b=1[/TEX]
=>pt của (d): [TEX]y=2x+1[/TEX]
c) (d) đi qua gốc tọa độ và tạo với trục Ox 1 góc 45 độ.
Giải: Ta có hệ số góc [tex]a=tan\alpha =tan45=1[/tex] => (d) có dạng: [TEX]y=x+b[/TEX]
Do (d) qua gốc tọa độ nên: [TEX]0=0+b<=>b=0[/TEX]
=> pt của (d) là: y=x
d) Tìm giao điểm của đường thẳng (d) tìm được ở câu b, với đường thẳng [TEX]y=3x+4[/TEX]
Giải: Khi tìm giao điểm, vì tọa độ của nó thỏa mãn đồng thời cả 2 phương trình, nên ta có phương trình hoành độ giao điểm: [TEX]2x+3=3x+4<=>x=-1[/TEX]
Thay x=-1 có [TEX]y=3.(-1)+4=1[/TEX]
Vậy tọa độ giao điểm cần tìm là A(-1;1)
Cơ bản là các dạng như vậy, chỉ cần nắm được lí thuyết là chúng ta có thể vận dụng để giải các bài tập của đề ra.