Xác định góc và tính góc trong không gian

T

tui_latui

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

:)>- phần này khá phổ biến trong thi cử vậy nên mình muốn đưa đề tài này ra để bàn luận .:):)
Mình mong ai có thắc mắc về vấn đề này về chỗ nào thì đưa lên để mọi người cùng tham khảo và rút kinh nghiệm nhé.
ai có bài nào không giải quyết được thì cứ post lên chúng ta cùng nghiên cứu.
Bởi vì vấn đề về góc ,mình thấy hay mà.:)>-:)>-
 
T

tui_latui

đây là bài toán ngược .ai có phương pháp giải bài toán loại này thì giúp mình với nha.
mình hay nản với những bài thế này lắm.
đề bài::
Cho hình vuông ABCD cạnh a ;tâm O;SA vuông góc với mp(ABCD).Tính SA theo a để mp(SBC) hợp với mp (SCD) một góc 120 độ
mình thì hay thấy những bài cho dữ kiện rồi tính góc chứ cho góc rồi xác định mà dựng thì trái xoáy quá
Ai có bí quyết gì không giúp mình với
Mình cảm ơn nhiều.
 
D

dongocthinh1

Cho hình vuông ABCD cạnh a ;tâm O;SA vuông góc với mp(ABCD).Tính SA theo a để mp(SBC) hợp với mp (SCD) một góc 120 độ

Capture-5.jpg


(SBC) và (SCD) cắt nhau theo giao tuyến SC

Để vẽ góc giữa 2 mặt phẳng này, ta tìm một mặt phẳng vuông góc với giao tuyến SC của chúng
Để tìm mặt phẳng đó, hãy để ý một đường thẳng chéo SC và vuông góc SC, đó là BD
Từ O kẻ OK vuông góc SC
=> (BKD) vuông góc SC
(BKD) cắt (SBC) và (SCD) theo giao tuyến BI và ID
=> góc tạo bởi hai mặt phẳng (SBC) và (SCD) là BID = 120*
Hai tam giác BSI và DSI bằng nhau ( SB=SD, SI chung, góc BSI = góc DSI do hai tam giác vuông CBS và CDS bằng nhau)
=> BI=ID => tam giác BID cân tại I
mà IO là trung tuyến => IO vuông góc BD
ta có: BKO=DKO=1/2BKD=60*
tanBKO = BO/OI => OI = BO/tanBIO = (a căn 2/2) / căn 3 = a căn 6 / 6
trong tam giác CIO:
CI=căn (CO^2 -OK^2) = a căn 12/12
Tam giác CIO đồng dạng CAS => CI/CA=IO/AS => AS = IO*CA/CI = a
 
D

dongocthinh1

Phương pháp xác định góc tạo bởi 2 mặt phẳng

Có 2 cách xác định.
Cách 1:

Capture-6.jpg

Giả sử 2 mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d
Tìm một mặt phẳng (R) vuông góc với giao tuyến d
(R) cắt (P) theo giao tuyến a
(R) cắt (Q) theo giao tuyến b
=> Góc tạo bởi hai mặt phẳng (P),(Q) là (a,b)

Cách 2: Cực kì quan trọng, phải nắm rõ vì bạn sẽ thường xuyên gặp nó !!!

Capture-7.jpg

Giả sử 2 mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d
Một đường thẳng a vuông góc với mặt phẳng (P) tại A và cắt mặt phẳng (Q) tại B
Từ B kẻ đường thẳng HB vuông góc d tại H
=> Góc tạo bởi 2 mặt phẳng là AHB

Chứng minh:
AB vuông góc (P) => AB vuông góc d
mà HB vuông góc d
=> d vuông góc (AHB)
(P) và (Q) cắt nhau theo giao tuyến d
(AHB) cắt (P) và (Q) theo giao tuyến HA và HB
=> góc tạo bởi (P) và (Q) là (AHB)
 
D

dongocthinh1

Ví dụ mẫu

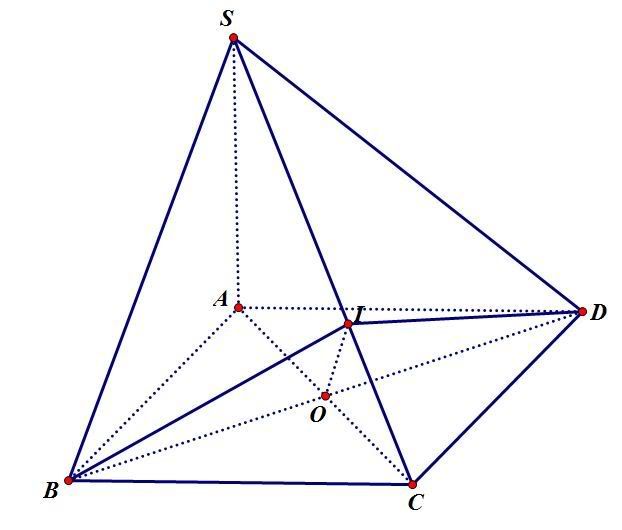
Cho hình chóp SABCD có SA vuông góc (ABCD) và SA = a căn 2. ABCD là hình thang vuông tại A và D, AB=2a, AD=DC=a.
Tính góc tạo bởi
a) (SBC) và (ABC)
b) (SAB) và (SBC)
c) (SBC) và (SCD)

Capture-8.jpg

a)
(SBC) và (ABC) cắt nhau theo giao tuyến BC
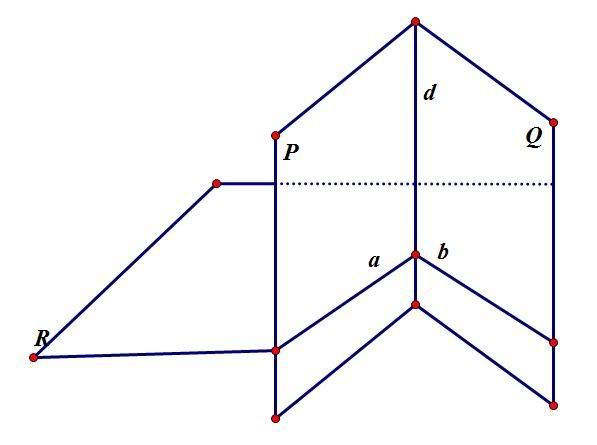
(ta đã có đường thẳng SA cắt (SCB) tại S và vuông góc (ABC) tại A, đúng như quang cảnh của phương pháp trên. Bây giờ chỉ việc từ S hoặc A kẻ vuông góc với giao tuyến BC là xong)
Gọi I là trung điểm AB => AICD là hình vuông
Ta có: CI=IA=IB => tam giác ACB vuông tại C hay AC vuông góc CB
Mặt khác: SA vuông góc CB => CB vuông góc (SAC)
=> góc tạo bởi hai mặt phẳng (SBC) và (ABC) là góc SCA.
TanSCA = SA/AC =1 =>SCA=45 độ
b)(SAB) và (SBC) cắt nhau theo giao tuyến SB
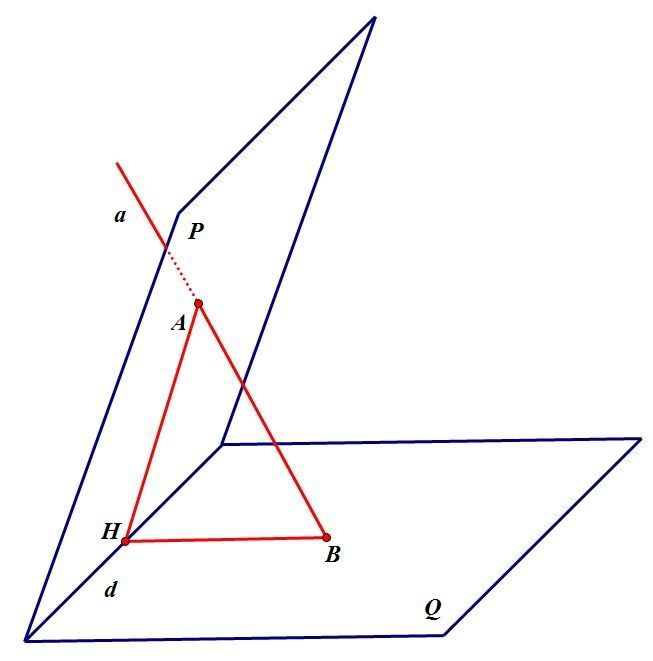
(Bây giờ tìm một đường thẳng vuông góc với một trong hai mặt phẳng đó và cắt mặt phẳng kia tại 1 điểm, ta nhận thấy CI vuông góc AB và SA nên CI vuông góc (SAB) mà CI cắt (SBC) tại C nên CI là đường thẳng cần tìm)

Ta có:
CI vuông góc (SAB)
từ I kẻ IK vuông góc SB, khi đó: CIK vuông góc (SBC)
Do đó, góc tạo bởi hai mặt phẳng (SAB) và (SBC) là góc CIK
Tam giác BKI và BAS đồng dạng
IK/AS=BI/BS => IK = a căn 3/3
trong tam gác vuông CKI ( vuông tại I):
tan CKI = CI/IK =căn 3 => CKI= 60 độ

c)(SBC) và (SCD) cắt nhau theo giao tuyến SC
cắt nhau theo giao tuyến SB
(]Bây giờ tìm một đường thẳng vuông góc với một trong hai mặt phẳng đó và cắt mặt phẳng kia tại 1 điểm là rất khó nên ta chuyển sang cách 1 là tìm một mặt phẳng vuông góc với SC bằng cách tìm một đường thẳng chéo SC và vuông góc SC rồi từ đường thẳng đó, kẻ vuông góc với SC là xong)
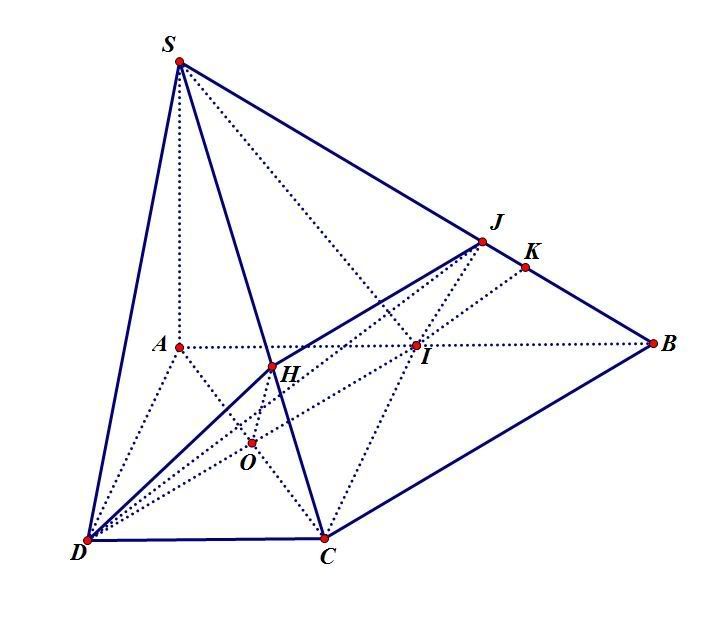
DI vuông góc (SAC) => DI vuông góc SC
Gọi O là giao điểm của DI và AC
Từ O kẻ OH vuông góc SC
=> (HDI) vuông góc SC

Ta có: DI thuộc (HDI)
BC không thuộc (HDI)
BC //DI
=> BC//(HDI)
Mặt phẳng (HDI) qua H cắt (SCB) theo giao tuyến HJ//CB ( J thuộc SB)

Do đó, góc tạo bởi hai mặt phẳng (SDC) và (SBC) là góc DHJ

tam giác CHO đồng dạng CAS
=> OH/AS=CO/CS => OH = a/2
Tam giác HDI cân tại H => HO vuông góc OD
=> HD = căn OH^2 +OD^2 = a căn 3 /2

HJ//BC => HJ/BC=SH/SC => HJ =...
Tam giác DIJ vuông tại I (tính IJ sẽ tính được DJ)
Rồi dùng định lý hàm số cos sẽ tính ra arcosDHJ = căn 6 / 3

(Bây giờ buồn ngủ quá, đi ngủ để mai còn sức đi học sớm, mọi người thông cảm, mình chỉ giải ngang đó thôi, còn lại gợi ý :eek: )
 
T

tui_latui

bạn à theo mình thì là tìm một đường thảng vuông góc với giao tuyến mà cắt 2 mặt thôi ? cần gì phải dựng mặt phẳng ?phải không?
 
N

nhocngo976

cách xác định góc giữa 2 mf



cho 2 mf [TEX](P) \cap (Q) = \Delta[/TEX]

cách 1: tìm mf (R) vuông góc với 2 mf , [TEX](R) \cap (P)= p, (R) \cap (Q)=q---> ((P);(Q))=goc \ giua\ (p,q)[/TEX][TEX][/TEX]

cách 2:chọn trên [TEX]\Delta [/TEX] điểm M, từ M kẻ [TEX]Mx \bot \Delta( Mx \ thuoc \ (P), My \bot \Delta ( My \ thuoc \ (Q)[/TEX]

\Rightarrow[TEX]((P);(Q))=goc \ giua \ (Mx;My)[/TEX]

cách 3: chọn trên (P) ( hoặc (Q)) điểm M, từ M kẻ [TEX]Mx \bot \Delta = N, ke \ Ny \bot \Delta ---> ((P);(Q))= goc \ giua \ (Mx;Ny)[/TEX]

cách 4: tìm đường thẳng [TEX]d \bot \Delta, d \cap (P)=A, d \cap (Q) =B[/TEX]

gọi O hình chiếu của A ( hoặc B) lên [TEX]\Delta [/TEX]---> [TEX]((P);(Q))= goc \ giua \ (AO,OB)[/TEX]

cách 5: tìm đường thẳng [TEX]d \bot (P) = A, d \cap (Q)=B----> O \ hinh \ chieu \ cua \ A \ hoac \ B \ len \ \Delta ----> ((P);(Q))=\ goc \ giua \ (OA;OB)[/TEX]

[TEX][/TEX][TEX][/TEX]
 
D

dongocthinh1

tui_latui said:
bạn à theo mình thì là tìm một đường thảng vuông góc với giao tuyến mà cắt 2 mặt thôi ? cần gì phải dựng mặt phẳng ?phải không?
Bấm để xem đầy đủ nội dung ...


Thật ra, bạn tìm đường thẳng a vuông góc vơi giao tuyến d và cắt 2 mặt phẳng [B(]đường thẳng này phải chéo giao tuyến ) [/B]
Rồi cũng từ đường thẳng d này kẻ vuông góc lên cắt giao tuyến a tại một điểm H.
Sau đó nối điểm H với giao điểm A,B của đường thẳng d và hai mặt phẳng trên

Làm thế là đúng nhưng bạn phải trình bày cho đúng định lý trong sách giáo khoa.
"Góc giữa hai mặt phẳng là góc tạo bởi hai đường thẳng vuông góc với 2 mặt phẳng đó"

Như vậy bạn phải chứng minh hai đường thẳng AH và BH lần lượt vuông góc với 2 mặt phẳng kia, như vậy mới kết luận góc AHB là góc tạo bởi 2 mặt phẳng.

Hoặc trong sách giáo khoa có trình bày một nhận xét
" Hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d, một mặt phẳng (R) vuông góc d và cắt (P) và (Q) theo giao tuyến a và b. Góc giữa 2 mặt phẳng chính là góc giữa hai đường thẳng a và b"


Dù làm gì đi nữa rồi cũng quy về chứng minh được một trong hai điều trên.

Việc chứng minh được 2 đường thẳng vuông lần lượt vuông góc với 2 mặt phẳng sẽ khó và dài hơn là dựng một mặt phẳng vuông góc với giao tuyến của 2 mặt phẳng kia rồi tìm giao tuyến của chúng.

Phương pháp mà mình dùng xác định góc giữa hai mặt phẳng là quy về từ nhận xét của SGK.
Bạn chỉ được áp dụng những định lý, tính chất, hệ quả ... nếu SGK có nói, còn không thì phải tự chứng minh mới được áp dụng :)
 
H

hoathuytinh16021995

to nghi la nhocngo976 k sai dau.vi trong mp dg thag a vuong goc voi giao tuyen d thi se vuong goc voi mp kia ma
 
You must log in or register to reply here.
Top Bottom