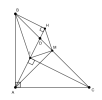
a.1) Xét [imath]M[/imath] là trung điểm của [imath]BC[/imath] [imath]\Rightarrow[/imath] [imath]AM[/imath] là đường trung tuyến của [imath]\Delta ABC[/imath].
Vì [imath]\Delta ABC[/imath] vuông cân tại [imath]A[/imath] ta có: [imath]AM[/imath] là đường phân giác của [imath]\Delta ABC[/imath]. [imath]\displaystyle \widehat{BAM}=\widehat{CAM}[/imath]
a.2) Ta thấy trong [imath]\Delta ABC[/imath] vuông tại [imath]A[/imath]: [imath]\displaystyle \widehat{DAB}+\widehat{DAC}=90\degree[/imath] (1)
Mặt khác: trong [imath]\Delta IAC[/imath] vuông tại [imath]I[/imath] ta có: [imath]\displaystyle \widehat{IAC}+ \widehat{ICA}=90\degree[/imath] (2)
(1) (2) [imath]\rightarrow[/imath] [imath]\displaystyle \widehat{BAH} = \widehat{ACI}[/imath]
Xét [imath]\Delta AIC[/imath] và [imath]\Delta BHA[/imath]:
+ [imath]\displaystyle \widehat{BHA}=\widehat{AIC}=90\degree[/imath]
+ [imath]\displaystyle \widehat{BAH}=\widehat{ICA}[/imath]
+ [imath]\displaystyle BA=CA\hspace{0.5cm} (gt)[/imath]
[imath]\Rightarrow \Delta AIC=\Delta BHA[/imath] (cạnh huyền - góc nhọn)
[imath]\Rightarrow BH=AI[/imath] (2 cạnh tương ứng)
b) Do[imath]\Delta ABC[/imath] vuông cân tại [imath]A[/imath] nên [imath]\displaystyle AM[/imath] là đường trung trực của [imath]BC[/imath] [imath]\Rightarrow AM \bot BC[/imath] (3)
* Chứng minh tương tự như câu a) ta có: [imath]\displaystyle \widehat{DAM}=\widehat{ICD}[/imath] <cùng phụ với [imath]\widehat{ADC}[/imath] (4)
Vì [imath]\Delta AHB=\Delta AIC[/imath] [imath]\Rightarrow AH=IC[/imath] (5)
Từ (3) (4) (5) [imath]\Rightarrow \Delta AHM = \Delta CIM[/imath] (c-g-c) [imath]\Rightarrow HM=MI[/imath] và [imath]\widehat{HMA}=\widehat{IMC}[/imath]
Mặt khác : [imath]\widehat{AMB}=\widehat{AMC}=90\degree[/imath]
[imath]\Rightarrow \widehat{HMB}=\widehat{IMA}[/imath]
* Tự chứng minh: [imath]\widehat{HMI}=90\degree[/imath]
[imath]\Rightarrow \Delta MHI[/imath] vuông cân tại [imath]M[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


