D
daotruong111
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
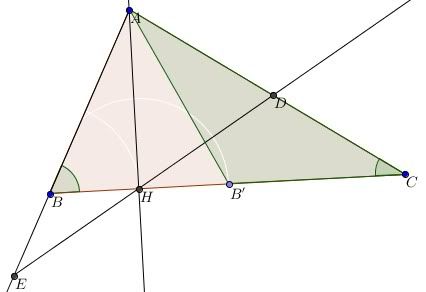
Cho $\triangle ABC; \widehat{B}< 90^o; \widehat{B}=2 \widehat{C}$. ĐƯờng cao AH, trên tia đối của BA lấy E sao cho $BE=BH$. HE cắt AC tại D
a) CM: $\widehat{ BEH}=\widehat{ACB}$
b) CM: $ DH=DC=DA$
c) Lấy B' sao cho H là trung điểm của BB'. CM: $ \triangle AB'C$ cân
d) CM: $AE=HC$
Chú ý: Viết Tiếng Việt có dấu. Sử dụng latex, học ở http://diendan.hocmai.vn/showthread.php?t=4917
P.S: Đã sửa
a) CM: $\widehat{ BEH}=\widehat{ACB}$
b) CM: $ DH=DC=DA$
c) Lấy B' sao cho H là trung điểm của BB'. CM: $ \triangle AB'C$ cân
d) CM: $AE=HC$
Chú ý: Viết Tiếng Việt có dấu. Sử dụng latex, học ở http://diendan.hocmai.vn/showthread.php?t=4917
P.S: Đã sửa
Last edited by a moderator: