- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. Phương pháp chung
- việc đổi điểm để tính khoảng cách trong không gian có thể đưa 1 bài toán phức tạp trở thành 1 bài toán nhẹ nhàng hơn.
- Phương pháp: cho 2 điểm A, B và mặt phẳng (P). ta có:
+ khi AB//(P): [tex]\frac{d(A,(P))}{d(B,(P))}=1<=>d(A,(P))=d(B,(P))[/tex]
+ khi AB cắt (P) tại M: theo Talet ta có: [tex]\frac{d(A,(P))}{d(B,(P))}=\frac{AM}{BM}<=>d(A,(P))=\frac{AM}{BM}.d(B,(P))[/tex]
* Nhận xét: - khi M là trung điểm AB thì [tex]\frac{d(A,(P))}{d(B,(P))}=\frac{AM}{BM}=1<=>d(A,(P))=d(B,(P))[/tex]
- mặt phẳng (P) cách đều 2 điểm phân biệt A, B khi AB//(P) hoặc mặt phẳng P đi qua trung điểm MN.
* ví dụ 1: cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=3a;AD=a. hình chiếu của S xuống mặt phẳng đáy là H nằm trên cạnh AB thỏa mãn HB=2.HA. biết SH=2a. tính khoảng cách từ A đến mặt phẳng (SBD).
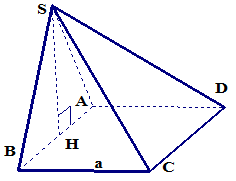
nếu ta đi theo hướng thuần túy là cứ cố định điểm A thì không dễ tìm được hình chiếu vuông góc lên mặt phẳng (SBD). bây giờ ta đổi điểm A về điểm H và tính. ta có:
[tex]\frac{HB}{AB}=\frac{1}{3}=>\frac{d(H,(SBD))}{d(A,(SBD))}=\frac{1}{3}<=>d(A,(SBD))=3.d(H,(SBD))[/tex]. như vậy, bây giờ ta chỉ cần tính khoảng cách từ H đến mặt (SBD). việc này rất dễ dàng. nếu gọi K là điểm thuộc BD sao cho HK//AD thì theo talet, ta có: [tex]\frac{HK}{AD}=\frac{BH}{AB}=\frac{1}{3}=>HK=\frac{a}{3}[/tex].
khi đó, ta có ngay tứ diện H.SBK là tứ diện vuông tại H. mà tứ diện vuông thì ta luôn có [tex]\frac{1}{d^2(H,(SBK))}=\frac{1}{HB^2}+\frac{1}{HK^2}+\frac{1}{SH^2}[/tex]
từ đó ta dễ dàng tính được khoảng cách cần tìm.
* Khoảng cách giữa 2 đường thẳng chéo nhau.
- việc tìm được đoạn vuông góc chung là 1 việc không dễ, một số bài toán thậm chí là không thể tìm được. vì vậy, ta phải xử lý theo 1 hướng khác.
- giả sử có 2 đường thẳng d và d' chéo nhau. ta cần tìm 1 mặt phẳng (P) đi qua d' và song song với d. khi đó, [tex]d(d,d')=d(d,(P))=d(M,(P))[/tex], với M là điểm bất kì thuộc d. khi đó, bài toán đưa về khoảng cách giữa điểm với mặt phẳng và có thể xử lý như phương pháp trên.
Ngoài ra, các bạn có thể tham khảo thêm các kiến thức liên quan nhé
Chinh phục kì thi THPTQG môn Toán 2022 ;
Tổng hợp những bài toán HHKG thường gặp
Giải chi tiết bài tập khoảng cách trong hình học không gian cổ điển
- việc đổi điểm để tính khoảng cách trong không gian có thể đưa 1 bài toán phức tạp trở thành 1 bài toán nhẹ nhàng hơn.
- Phương pháp: cho 2 điểm A, B và mặt phẳng (P). ta có:
+ khi AB//(P): [tex]\frac{d(A,(P))}{d(B,(P))}=1<=>d(A,(P))=d(B,(P))[/tex]
+ khi AB cắt (P) tại M: theo Talet ta có: [tex]\frac{d(A,(P))}{d(B,(P))}=\frac{AM}{BM}<=>d(A,(P))=\frac{AM}{BM}.d(B,(P))[/tex]
* Nhận xét: - khi M là trung điểm AB thì [tex]\frac{d(A,(P))}{d(B,(P))}=\frac{AM}{BM}=1<=>d(A,(P))=d(B,(P))[/tex]
- mặt phẳng (P) cách đều 2 điểm phân biệt A, B khi AB//(P) hoặc mặt phẳng P đi qua trung điểm MN.
* ví dụ 1: cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=3a;AD=a. hình chiếu của S xuống mặt phẳng đáy là H nằm trên cạnh AB thỏa mãn HB=2.HA. biết SH=2a. tính khoảng cách từ A đến mặt phẳng (SBD).
nếu ta đi theo hướng thuần túy là cứ cố định điểm A thì không dễ tìm được hình chiếu vuông góc lên mặt phẳng (SBD). bây giờ ta đổi điểm A về điểm H và tính. ta có:
[tex]\frac{HB}{AB}=\frac{1}{3}=>\frac{d(H,(SBD))}{d(A,(SBD))}=\frac{1}{3}<=>d(A,(SBD))=3.d(H,(SBD))[/tex]. như vậy, bây giờ ta chỉ cần tính khoảng cách từ H đến mặt (SBD). việc này rất dễ dàng. nếu gọi K là điểm thuộc BD sao cho HK//AD thì theo talet, ta có: [tex]\frac{HK}{AD}=\frac{BH}{AB}=\frac{1}{3}=>HK=\frac{a}{3}[/tex].
khi đó, ta có ngay tứ diện H.SBK là tứ diện vuông tại H. mà tứ diện vuông thì ta luôn có [tex]\frac{1}{d^2(H,(SBK))}=\frac{1}{HB^2}+\frac{1}{HK^2}+\frac{1}{SH^2}[/tex]
từ đó ta dễ dàng tính được khoảng cách cần tìm.
* Khoảng cách giữa 2 đường thẳng chéo nhau.
- việc tìm được đoạn vuông góc chung là 1 việc không dễ, một số bài toán thậm chí là không thể tìm được. vì vậy, ta phải xử lý theo 1 hướng khác.
- giả sử có 2 đường thẳng d và d' chéo nhau. ta cần tìm 1 mặt phẳng (P) đi qua d' và song song với d. khi đó, [tex]d(d,d')=d(d,(P))=d(M,(P))[/tex], với M là điểm bất kì thuộc d. khi đó, bài toán đưa về khoảng cách giữa điểm với mặt phẳng và có thể xử lý như phương pháp trên.
Ngoài ra, các bạn có thể tham khảo thêm các kiến thức liên quan nhé
Chinh phục kì thi THPTQG môn Toán 2022 ;
Tổng hợp những bài toán HHKG thường gặp
Giải chi tiết bài tập khoảng cách trong hình học không gian cổ điển
Last edited by a moderator:
