[hình 8] Chứng minh vuông góc

[cao_boi_texas9x_thansung@yahoo.com.vn]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

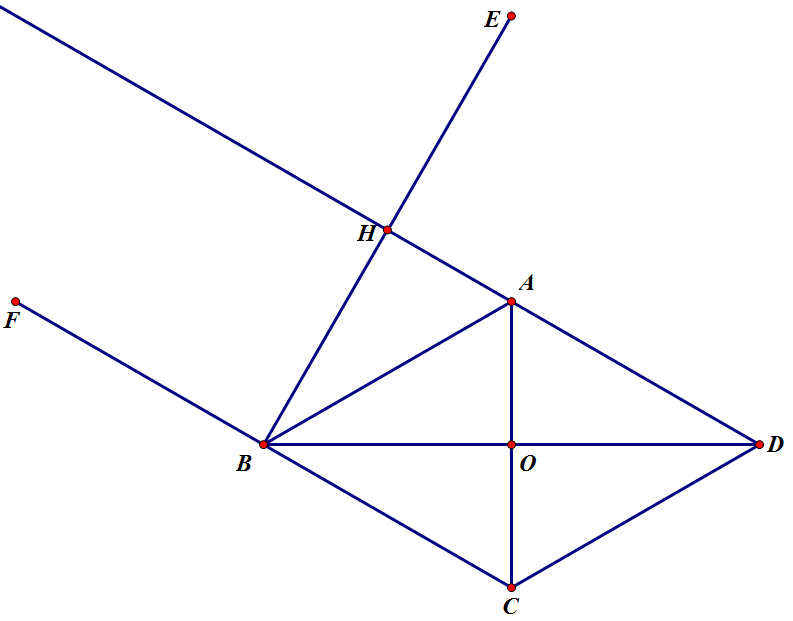
Hình thoi ABCD có góc A=60 độ, đường cao BH vuông góc với AD. E đối xứng với B qua H, F đới xứng với C qua B, AC cắt BD tại O. Ak vuông góc với OE, N là trung điểm của EK. Chứng minh DN vuông góc với KF

 

[demon311]

ĐỘI 5

Đề sai hoặc thiếu

$AK \perp OE$ nhưng K nằm ở đâu? $AK \equiv OE$ mà

 

[thienbinhgirl]

ĐỘI 5

Đề sai hoặc thiếu

$AK \perp OE$ nhưng K nằm ở đâu? $AK \equiv OE$ mà

GÓC a = 60* MÀ ANH........................................................................................

 

[phamvananh9]

ĐỘI 5

Đề sai hoặc thiếu

$AK \perp OE$ nhưng K nằm ở đâu? $AK \equiv OE$ mà

[TEX][/TEX]
a ơi góc A bằng 60 độ mà, đề đúng rùi!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

 

[thienbinhgirl]

đội 5

$\Delta AHE=\Delta DHB(c.g.c)\rightarrow AE//BD; AE=BD $ (*)
$\Delta ACF$ có AB=BE=BC \Rightarrow $\Delta ACF$ vuông \Rightarrow AF=DB và AF//DB
Từ trên \Rightarrow 3 điểm E ,A , F thẳng hàng có N là trung điểm của EK (1)
Trong tam giác AHB vuông có góc A = 60 độ \Rightarrow $AH=\frac{1}{2}HB\rightarrow HB=2AH$ mà BF=2AH ( áp dụng đường trung bình ) \Rightarrow HB=BF mà BI vuông góc với HF \Rightarrow BI là đường trung trực trong tam giác HBF \Rightarrow KI=IF (2)
Từ (1)(2) \Rightarrow NI//EF và $NI=\frac{1}{2}EF$ \Rightarrow NI//EA và NI=EA(*)(*)
Từ(*)và (*)(*)\Rightarrow NIBD là hình bình hành mà IB vuông góc KF \Rightarrow KF vuông góc với ND

 

[demon311]

ĐỘI 5

$\Delta AHE=\Delta DHB(c.g.c)\rightarrow AE//BD; AE=BD $ (*)
$\Delta ACF$ có AB=BE=BC \Rightarrow $\Delta ACF$ vuông \Rightarrow AF=DB và AF//DB
Từ trên \Rightarrow 3 điểm E ,A , F thẳng hàng có N là trung điểm của EK (1)
Trong tam giác AHB vuông có góc A = 60 độ \Rightarrow $AH=\frac{1}{2}HB\rightarrow HB=2AH$ mà BF=2AH ( áp dụng đường trung bình ) \Rightarrow HB=BF mà BI vuông góc với HF \Rightarrow BI là đường trung trực trong tam giác HBF \Rightarrow KI=IF (2)
Từ (1)(2) \Rightarrow NI//EF và $NI=\frac{1}{2}EF$ \Rightarrow NI//EA và NI=EA(*)(*)
Từ(*)và (*)(*)\Rightarrow NIBD là hình bình hành mà IB vuông góc KF \Rightarrow KF vuông góc với ND

Anh bổ sung chút: I là trung điểm của FK nhé

 

[0973573959thuy]

$\Delta AHE=\Delta DHB(c.g.c)\rightarrow AE//BD; AE=BD $ (*)
$\Delta ACF$ có AB=BE=BC \Rightarrow $\Delta ACF$ vuông \Rightarrow AF=DB và AF//DB
Từ trên \Rightarrow 3 điểm E ,A , F thẳng hàng có N là trung điểm của EK (1)
Trong tam giác AHB vuông có góc A = 60 độ \Rightarrow $AH=\frac{1}{2}HB\rightarrow HB=2AH$ mà BF=2AH ( áp dụng đường trung bình ) \Rightarrow HB=BF mà BI vuông góc với HF \Rightarrow BI là đường trung trực trong tam giác HBF \Rightarrow KI=IF (2)
Từ (1)(2) \Rightarrow NI//EF và $NI=\frac{1}{2}EF$ \Rightarrow NI//EA và NI=EA(*)(*)
Từ(*)và (*)(*)\Rightarrow NIBD là hình bình hành mà IB vuông góc KF \Rightarrow KF vuông góc với ND

Cho tớ hỏi Sao trong tam giác AHB vuông tại H có AH = 1/2 HB nhỉ

 

[thienbinhgirl]

Cho tớ hỏi Sao trong tam giác AHB vuông tại H có AH = 1/2 HB nhỉ

H là trung điểm của EB ( E đối xứng với B qua H ) HA//CF \Rightarrow HA là đường trung bình trong tam giác EBF \Rightarrow AH = 1/2 HB