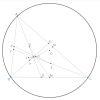
Dễ dàng chứng minh [imath]MX,NY,PZ[/imath] đồng quy tại [imath]G[/imath] bằng định lý Céva.
Gọi [imath]Mt[/imath] là điểm Mittenpunkt của [imath]\Delta ABC[/imath].
Có một kết quả liên quan đến điểm này là [imath]L,I,Mt[/imath] thẳng hàng (em có thể xem chứng minh ở trên mạng nhé)
Từ đây ta chỉ cần chứng minh [imath]I,Mt,G[/imath] thẳng hàng.
Nhận thấy nếu gọi [imath]I_a,I_b,I_c[/imath] là các tâm đường tròn bàng tiếp góc [imath]A,B,C[/imath] của [imath]\Delta ABC[/imath] thì [imath]Mt[/imath] là điểm Lemoine của [imath]\Delta I_aI_bI_c[/imath]. Mà dễ thấy [imath]I_aM,I_bN,I_cP[/imath] là đường đối trung của [imath]\Delta I_aI_bI_c[/imath] nên [imath]I_aM,I_bN,I_cP[/imath] đồng quy tại [imath]Mt[/imath].

+ Chứng minh [imath]YZ,NP,I_bI_c[/imath] đồng quy.
Gọi [imath]H,J[/imath] lần lượt là giao điểm của [imath]PN,BC[/imath] với [imath]I_bI_c[/imath]. Khi đó dễ thấy [imath]H[/imath] là trung điểm [imath]AJ[/imath].
Vì [imath]I_aA,I_bB,I_cC[/imath] đồng quy trong [imath]\Delta I_aI_bI_c[/imath] nên [imath](JA,I_cI_b)=-1[/imath]
[imath]\Rightarrow I_a(JA,I_cI_b)=-1 \Rightarrow (JD,BC)=-1[/imath] (chiếu trên đường thẳng [imath]BC[/imath])
Mặt khác, [imath]AD,BE,CF[/imath] đồng quy trong [imath]\Delta ABC[/imath] nên [imath]J,E,F[/imath] thẳng hàng.
Từ đó [imath]H,Y,Z[/imath] thẳng hàng theo đường thẳng Gauss của tứ giác toàn phần [imath]BFEC.AJ[/imath]
+ Chứng minh [imath]I,G,Mt[/imath] thẳng hàng.
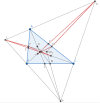
Áp dụng định lý Desargues cho [imath]\Delta YNI_b[/imath] và [imath]\Delta ZPI_c[/imath] có [imath]YZ,NP,I_bI_c[/imath] thẳng hàng ta có [imath]I,G,Mt[/imath] thẳng hàng.
(Lời giải: Chu Văn Linh - T1K31 - THPT Chuyên Hà Tĩnh)
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
Đề thi ôn tập chọn HSGQG [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.