Nếu phải tóm tắt lại lịch sử phát triển hơn 200 năm của đạo hàm chỉ trong một câu thì tôi sẽ trích dẫn lời của tác giả Grabiner: “
Đạo hàm đầu tiên được sử dụng như công cụ, sau đó mới được phát minh, tiếp nữa là được mở rộng và phát triển, cuối cùng mới được định nghĩa.” Thế nghĩa là thế nào? Nghĩa là trước khi được phát minh ra, người ta đã biết cách sử dụng nó như một công cụ đầy hiệu quả. Để hiểu đầu cua tai nheo thì chúng ta phải quay trở về những năm 1630 để tìm hiểu một phương pháp tìm cực trị mới mẻ mà Fermat đã nghĩ ra:
Ông xét bài toán sau: Cho trước một đoạn thẳng, hãy chia nó thành 2 phần sao cho tích của 2 phần này là lớn nhất
Đáp án của bài toán này thì người ta đã biết từ trước (tích lớn nhất khi ta chia đoạn thẳng thành 2 phần bằng nhau) nhưng cách làm của Fermat thì lại rất mới. Gọi chiều dài đoạn ban đầu là B, chiều dài đoạn thứ nhất là A thì chiều dài đoạn thứ hai sẽ là:B-A và tích của 2 phần là:
.
Nhà toán học Hi Lạp Pappus ở Alexandria trong một tác phẩm của mình có đưa ra một nguyên lý: “Một bài toán nào đó nói chung có 2 nghiệm thì nó sẽ đạt được giá trị cực đại (hoặc cực tiểu) trong trường hợp chỉ có một nghiệm”. Tôi sẽ dành một chút thời gian để minh họa nguyên lí này của Pappus bởi vì đây là một nguyên lí rất thú vị và có ích:
Xét bài toán đơn giản sau: Từ điểm A nằm ngoài đường thẳng d cho trước, hãy xác định điểm N trên d sao cho độ dài đoạn AN là nhỏ nhất?
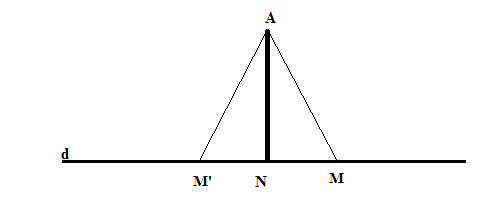
Bây giờ chúng ta hãy giả vờ khờ khạo không biết điểm N cần tìm ở đâu, lúc này hãy giả sử chúng ta tìm được một điểm M nào đó nằm bên phải thõa mãn yêu cầu đề bài (tức là làm cho đoạn AM nhỏ nhất). Khi đó nói chung luôn có một điểm M’ nằm bên trái để cho AM = AM’ cho nên nếu M là nghiệm của bài toán này thì M’ cũng phải là nghiệm và bài toán sẽ luôn có 2 nghiệm. Nguyên lý Pappus phát biểu rằng, giá trị cực tiểu sẽ đạt được trong trường hợp chỉ có một nghiệm, mà muốn vậy thì
. Điều này chỉ xảy ra khi M chính là chân đường vuông góc kẻ từ A xuống d và đây cũng chính là đáp án của bài toán này. Ví dụ này mặc dù khá tầm thường nhưng nguyên lí của Pappus thì lại rất hữu ích trong nhiều trường hợp tìm cực trị khác nhau. Nào bây giờ hãy trở lại với Fermat:
Ông giả sử rằng bài toán trên còn có thêm một đáp số thứ hai nữa (tức là có một cách chia khác để tích hai đoạn lớn nhất), với đáp số thứ hai này chúng ta sẽ gọi đoạn thứ nhất là
khi đó đoạn còn lại là:
. Tích của chúng lúc này bằng:
.
Bởi vì giá trị lớn nhất phải là duy nhất cho nên hai đáp số trên đều phải cho ra tích giống nhau, nghĩa là:
.
Rút gọn 2 vế cho E ta được:
Mặt khác theo nguyên ly Pappus thì 2 nghiệm này trong trường hợp đạt giá trị lớn nhất phải trở nên bằng nhau nên nói chung E không hề tồn tại. Thế là Fermat cho E = 0, từ đó ông thu được kết quả
, mà đây cũng chính là đáp số của bài toán trên. Cách làm của Fermat có cái gì đó vừa độc đáo vừa kì quái, ông giả sử rằng bài toán có 2 nghiệm và chúng khác nhau một lượng E. Lúc đầu ông xem E khác 0 và rút gọn E ở hai vế, sau đó ông ta vận dụng nguyên lí Pappus và nói rằng muốn đạt được cực trị thì nói chung E không nên tồn tại và thế là cho E = 0 cuối cùng lại thu được đáp số chính xác. Nếu bạn thấy cách làm này thật quái lạ thì bạn giống với đa số các nhà toán học thời kì đó, còn với thì hiện tại khi mà chúng ta đã học về đạo hàm tôi sẽ chỉ rõ để các bạn hiểu được rốt cuộc thì Fermat đã làm cái gì để giải được bài toán đó.
Bài toán mà Fermat giải là xác định
để hàm số
lớn nhất, và việc Fermat xem
sau đó rút gọn biểu thức cho
rồi cho
nếu nói theo ngôn ngữ ngày nay là ông đã sử dụng đặc trưng sau đây của hàm số tại điểm cực trị của nó:
Nếu bạn đã học lớp 12 thì chắc đã được nghe đến định lí Fermat về điều kiện cần để hàm số đạt cực trị rồi chứ. Vâng, chính nó đấy! Nhưng vào thời điểm này Fermat chưa biết đạo hàm là gì đâu, dù vậy có một sự kiện lý thú là Fermat đã ứng dụng phương pháp này vào các bài toán vật lí và thu được những kết quả rất phù hợp. Cụ thể ông đã áp dụng trong quang học: Fermat phát biểu một nguyên lý về cách “hành xử” của ánh sáng (nguyên lý tác dụng tối thiểu): “Ánh sáng luôn đi theo con đường nhanh nhất”. Theo nguyên lý này và khảo sát đường đi của ánh sáng ngang qua bề mặt phân cách của hai môi trường trong suốt đồng tính ông đã tìm con đường nhanh nhất của ánh sáng (bằng phương pháp mới ở trên) , chính là con đường tuân theo định luật Snell về khúc xạ (vốn đã tìm ra trước đó bằng thực nghiệm)/
Nếu có thời gian bạn hãy đọc thêm bài viết “Tự nhiên là nhà toán học” của tôi để hiểu thêm nhé.
Giai đoạn tiếp theo là thời điểm đạo hàm được phát minh. Đạo hàm ra đời lấy cảm hứng từ hai nguồn động lực chính. Động lực này đến từ nhu cầu phải giải quyết hai bài toán quan trong trong hai lĩnh vực khác nhau. Một đến từ hình học đó là bài toán xác định tiếp tuyến của đường cong và một đến từ vật lí là bài toán xác định vận tốc tức thời của chất điểm. Cùng tìm hiểu nhé…
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
