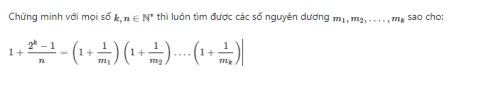Xét các trường hợp:
+ [imath]n \not \vdots 2[/imath]
Ta sẽ chứng minh quy nạp theo [imath]k[/imath].
Dễ thấy [imath]k=1[/imath] ta có đpcm.
Giả sử đpcm đúng với [imath]k=i \geq 1[/imath]. Ta đi chứng minh đpcm đúng với [imath]k=i+1[/imath]
Với [imath]n=2j-1 (j \in \mathbb{N}^*)[/imath], ta có [imath]1+\dfrac{2^{i+1}-1}{2j-1}=(1+\dfrac{1}{2j-1})(1+\dfrac{2^i-1}{j})[/imath] (bạn có thể tự kiểm tra lại đẳng thức này)
Theo giả thiết quy nạp, vì [imath]1+\dfrac{2^i-1}{j}[/imath] viết được thành [imath](1+\dfrac{1}{m_1})(1+\dfrac{1}{m_2})...(1+\dfrac{1}{m_i})[/imath] nên
[imath]1+\dfrac{2^{i+1}-1}{2j-1}=(1+\dfrac{1}{m_1})(1+\dfrac{1}{m_2})...(1+\dfrac{1}{m_i})(1+\dfrac{1}{2j-1})[/imath]
Từ đó đpcm đúng với [imath]k=i+1[/imath]. Theo nguyên lý quy nạp ta có đpcm đúng với mọi [imath]k \in \mathbb{N}^*[/imath].
+ [imath]n \vdots 2[/imath]. Ta viết [imath]n=2^j\cdot s[/imath] với [imath]s \not \vdots 2[/imath]
Ta sẽ chứng minh quy nạp theo [imath]j[/imath].
Với [imath]j=1[/imath] ta có [imath]1+\dfrac{2^k-1}{2s}=1+\dfrac{2^{k-1}-1}{s}+\dfrac{1}{2s}=(1+\dfrac{2^{k-1}-1}{s})(1+\dfrac{1}{2s+2(2^{k-1}-1)})[/imath]
Vì [imath]1+\dfrac{2^{k-1}-1}{s}[/imath] biểu diễn được thành [imath](1+\dfrac{1}{m_1})(1+\dfrac{1}{m_2})...(1+\dfrac{1}{m_{k-1}})[/imath] nên
[imath]1+\dfrac{2^k-1}{2s}=(1+\dfrac{1}{m_1})(1+\dfrac{1}{m_2})...(1+\dfrac{1}{m_{k-1}})(1+\dfrac{1}{2s+2(2^{k-1}-1)})[/imath]
Suy ra đpcm đúng với [imath]j=1[/imath]
Giả sử đpcm đúng với [imath]j=h \geq 1[/imath]. Ta đi chứng minh đpcm đúng với [imath]j=h+1[/imath].
Ta có [imath]1+\dfrac{2^k-1}{2^{h+1}s}=1+\dfrac{2^{k-1}-1}{2^hs}+\dfrac{1}{2^{h+1}s}=(1+\dfrac{2^{k-1}-1}{2^hs})(1+\dfrac{1}{2^{h+1}s+2(2^{k-1}-1)})[/imath]
Vì theo giả thiết quy nạp, [imath]1+\dfrac{2^{k-1}-1}{2^hs}[/imath] viết được thành [imath](1+\dfrac{1}{m_1})(1+\dfrac{1}{m_2})...(1+\dfrac{1}{m_{k-1}})[/imath] nên
[imath]1+\dfrac{2^k-1}{2^{h+1}s}=(1+\dfrac{1}{m_1})(1+\dfrac{1}{m_2})...(1+\dfrac{1}{m_{k-1}})(1+\dfrac{1}{2^{h+1}s+2(2^{k-1}-1)})[/imath]
Từ đó đpcm đúng với [imath]j=h+1[/imath].
Theo nguyên lý quy nạp, đpcm đúng với mọi [imath]j \in \mathbb{N}^*[/imath].
Chứng minh hoàn tất!
Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo kiến thức tại
[Lý thuyết] Chuyên đề HSG: Toán rời rạc [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.